El estudio de la matemática siempre ha estado lleno de controversia. Siempre han estado las personas que piensan que la matemática no se estudia, "se nace con eso" o directamente no servís. Bueno, vengo acá a explicarles que no, eso es mentira.
No me gusta quedarme con solo decir que no sin dar una explicación. Existe un porqué detrás de estas palabras.
Primero me gustaría dividir la matemática de primaria, la matemática de secundaria y la matemática universitaria. Sin tener en cuenta, obviamente, que tipo de matemática usted estará utilizando en su formación universitaria. Claramente no sera la misma la que pueda utilizar un Sociólogo (Mas orientado al análisis estadístico) que un Matemático (con sus mas complicadas y rigurosas ramas). Se explicara mas detalladamente luego.
 |
| Gráficos, Toma de datos, Análisis de diferentes variables. |
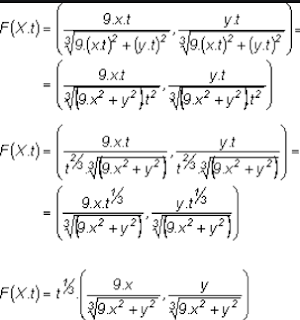 |
| Conceptos matemáticos abstractos, funciones y sistemas complejos. |
Prosigo contándoles una anécdota de índole personal. En la primaria, la matemática se me daba "normal", ni bien ni mal. Digamos que el desempeño era de esa índole, ya que no desaprobaba ninguna tarea o evaluación del colegio. De todas maneras, tampoco es que tuviera mucho interés en su estudio, obviamente a los 7/8/9 años estaba mas enfocado en el juego de videojuegos, computadora, juegos de mesa, juguetes, de todo menos estudiar. Como cualquier chico normal. Sin embargo, en 6to de primaria, viendo videos "curiosos" llegue a uno muy particular que se denominaba "Relatividad General explicación sencilla" o algo asi. En el cual explicaba los diferentes fenómenos físicos que ocurrían en esta teoría Matemático-Física de la ciencia. Sin la necesidad de saber matemática me encontraba disfrutando de una teoría maravillosa y muy avanzada técnicamente hablando.
De una forma u otra, termine intentando sacar mis propias conclusiones de la relatividad general. El problema era que si quería saber mas detalles y entenderla realmente como era necesario, necesitaba saber matemática. Nada iba a saber yo de integrales, derivadas parciales y todas esas cosas. Pero mientras todos aprendían como multiplicar, a mi que en ese momento se me daba fácil, me puse a aprender la potencia y la raíz. (La raíz se me hizo muuuucho mas dificultosa que la potencia pero me hizo entender que siempre hay una ida y vuelta. La suma tiene la resta, la division tiene la multiplicación, la potencia tiene la raíz). Este es un concepto que no se enseña usualmente en los colegios de educación primaria y es fácilmente entendible por qué. Sin interés, no se pueden apresurar los conceptos.
Mas tarde, durante la secundaria, hubo años buenos y años malos en el aprendizaje. Me di cuenta que en ese momento, pasaba mucho por no tenerle miedo a los conceptos que en un primer momento parecen complicados.
Una idea que revivia en aquel entonces fue el interés. Cuando no se genera interés en algo, es mucho mas difícil de aprenderlo.
Se dice que el profesor tiene toda la culpa y puedo decir si y no. Considero que tiene una importancia relevante para expresar de manera adecuada los conocimientos y para la elección de los ejemplos mas importantes que sinteticen de la mejor manera posible lo que se intenta enseñar. Sin embargo, la matemática es una representación abstracta de la realidad y todo lo que sea abstracto requiere de un trabajo mental.
Entonces, me gustaría desmitificar el hecho de que la matemática es un "todo complejo", como se piensa comúnmente.
Cómo una persona que esta Estudiando ingeniería y aprobó todos los cursos de matemática casi sin ningún problema, desaprobó muchísimos exámenes en la secundaria?
Normalmente la gente que desaprueba los examenes de este rubro suele pensar que no puede/no sirve para estudiar nada relacionado con esto ultimo. Bueno, eso es mentira. Por que? Porque a mi me paso! El aprendizaje es un conjunto de condiciones que se tienen que dar en diferentes proporciones.
1- Es importante generar interés en lo que se estudia. Siempre que estemos intentando incorporar algún concepto matemático, desde restas y sumas, hasta ecuaciones diferenciales a derivadas parciales de multiples variables, se necesita saber para que es utilizado dicho concepto. Esto nos otorga motivación. La motivación es la fuerza que nos hará imparables.
2- Es necesario que usemos varias fuentes de información. Por suerte para todos, el internet nos otorga una gran ventaja. Hay que utilizar todos los medios necesarios para comprender lo que se estudia. No sirve estudiar de memoria. La matemática se piensa, no se aprende "mecánicamente". Se pueden utilizar los videos de los miles de maestros en youtube, blogs como este, libros técnicos, libros no tan técnicos, libros de ejemplos, diferentes maestros reales, etc. Lo importante es identificar cual es el medio que mas nos ayuda a comprender dichos conceptos.
3- Una vez que se comprende un concepto, ya tenemos casi todo el camino completo. Considero que aprender matemática es muy fácil porque una vez que comprendemos el concepto solo hay que aprender las excepciones a la regla. Si es que existen claro. Ya que normalmente un teorema matemático, axioma o lo que sea, funciona porque cumple determinadas reglas. Por lo que si comprendemos las reglas y el funcionamiento de dichas reglas, el resto sale solo. Normalmente queda seguir los pasos del teorema como si de una receta se tratase.
4- Para aprender las excepciones normalmente hay que realizar ejercicios y volvernos rápidos. El volvernos rápidos con algún tipo en especial de resolución, nos hará terminar de dar cuenta como se utiliza dicho teorema, regla o lo que sea y el alcance que tiene a fondo.
5- Ultimo y no menos importante. Todos pueden aprender, solamente hay que seguir las reglas. Cada uno tendrá sus diferentes variaciones en cuanto a que método les resulta mas fácil para aprender. Tener confianza.
En mi caso particular, voy a las clases y escucho lo que tenga el profesor para decir. Quiza haya cosas que en el momento no termine de entender, pero un vistazo rápido ayuda para que cuando los leo de un libro técnico y me den una segunda explicación (el libro) entendiendo aun mas el alcance del teorema. Cuando realizo los ejercicios, analizo los ejemplos e intento imitarlos. Si hay algún ejercicio que no sale, preguntar a alguien que ya lo tenga hecho para analizar su resolución ayuda mucho. Por ultimo, vuelvo al teorema que al principio era incomprendido y todo tiene sentido.















