Función Lineal-Ecuación de la Recta

Enunciado:

 es una función lineal si es de la forma , para cada  donde m y b son números reales constantes.

La gráfica de cualquier  es una recta.

La ecuación y=mx+b se denomina ecuación explicita de la recta.

Raíz de una función lineal:

Diremos que r es raiz de una funcion lineal  tal que , con  si y solo si f(r)=0

Conjunto dominio y conjunto imagen:

Su dominio es R porque es el conjunto mas amplio de números reales el cual la formula tiene sentido.

La imagen de una función lineal es R.

Pendiente y ordenada al origen:

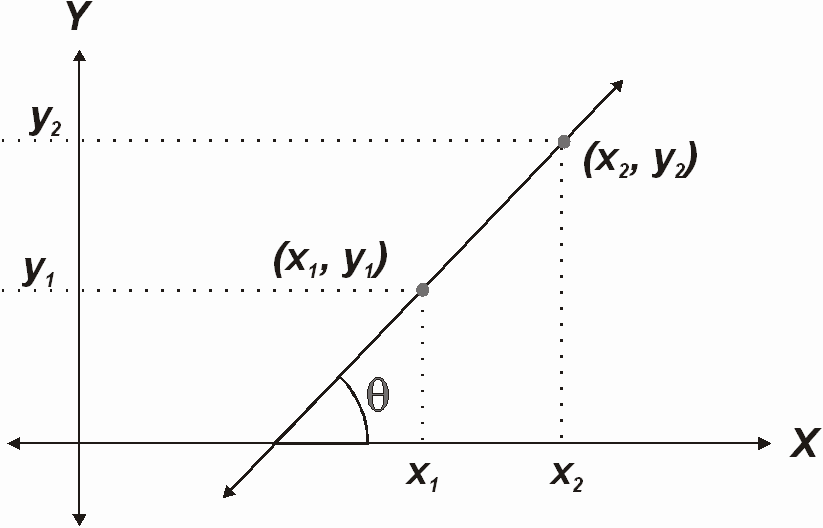
Entendemos por pendiente de una recta el "numero de unidades que la recta sube o baja por cada unidad de cambio horizontal de izquierda a derecha."

• Consideremos los puntos (x1,y1) y (x2,y2) de la recta.

Por lo tanto "m" es:

La pendiente esta relacionada con el angulo de inclinación de la recta con respecto al eje x.

Se puede apreciar que .

La pendiente también puede llamarse coeficiente angular.

Si la pendiente es positiva entonces la función es creciente.
Si la pendiente es negativa entonces la función es decreciente.
Si la pendiente es 0 entonces la función es constante.

Gráficas:

Si conocemos la pendiente y la ordenada al origen de una recta, resulta conveniente seguir estos procesos para graficar:

1. Colocar la ordenada al origen. Es el punto por el cual la recta cortara al eje y.
2. Interpretación de la pendiente. 
3. Trazar la recta.

Rectas que pasan por el origen:

Son de la forma: 

Es decir, su ordenada al origen es b=0.

Rectas horizontales:

Son de la forma:

Es decir, su pendiente m=0.

Rectas verticales:

Las rectas verticales No representan una función lineal.

Todos sus puntos tienen la misma abscisa, luego la ecuación que le corresponde es:

Rectas Paralelas y Perpendiculares:

Rectas paralelas:

Si dos rectas son paralelas, el angulo que forman con el eje positivo de las x sera el mismo, por lo tanto tendrán la misma pendiente.

Es decir: m1=m2

• Si b1=b2 entonces L1 y L2 son rectas paralelas coincidentes.

Rectas perpendiculares:

Dos rectas paralelas son aquellas que, en el punto de intersección, determinan ángulos rectos.

Es decir: 

Siempre y cuando m1 y m2 sean distintas de cero. 

• Las rectas horizontales son perpendiculares a las verticales.

Ecuaciones de una recta dada la pendiente y un punto o dados dos puntos.

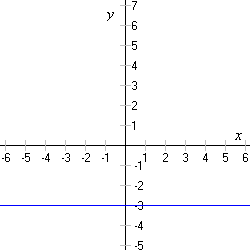
Dada la imagen, podemos definir los puntos P1 y P2. Siendo P1=(1,2) y P2=(2,4).

Segun la ecuacion para el calculo de pendiente  reemplazamos los valores de x1,y1 e x2,y2 y calculamos la pendiente. Nos da m=2. 

Ahora tenemos la ecuación de la siguiente manera: y=2x+b. 

Sabemos que la ordenada al origen (b), es aquel punto donde x=0. Mirando el gráfico donde x=0, y=0 entonces la ordenada al origen =0. 

Otra manera de hacer el calculo, es reemplazar por uno de los dos puntos que tenemos y verificar b.

Si reemplazamos por P1.

2=2.1+b

2-2=b

0=b

El razonamiento simplificado es el siguiente:

Forma punto-pendiente de una ecuacion de una linea recta.

Una ecuación de la recta con pendiente m y que pasa por el punto (x1,y1) es: 

Verificar por su propia cuenta.

Ecuación segmentaria y general de una recta.

La ecuación segmentaria de la recta tiene la forma:

"p" da el valor de la intersección con el eje x y "q" da el valor de la intersección con el eje y.

Las rectas horizontales, verticales y las que pasan por el origen, NO tienen una representación segmentaria.

Ecuación General-Forma Implicita

La ecuación general de la recta tiene la forma:

Ax+By+C=0 con A, B, C reales y A y B no simultaneamente nulos.