Llamamos función cuadrática a toda función  tal que
tal que 
donde a, b, c son números reales, siendo  .
.
El dominio de esta función es el conjunto de los números reales. Y su gráfica asociada a una función cuadratica es una parábola de eje vertical.

Graficar
Si  la parábola apunta hacia arriba.
la parábola apunta hacia arriba.
Si  la parábola apunta hacia abajo.
la parábola apunta hacia abajo.
- La grafica de
se obtiene recorriendo VERTICALMENTE de k unidades de la gráfica de
. Si k es positivo se movera hacia arriba, y si k es negativo se movera hacia abajo.
- La gráfica de
se obtiene con un movimiento HORIZONTAL de h unidades. Si h es positivo se movera a la derecha y si h es negativo se movera a la izquierda.
- La gráfica de
es la gráfica de
corrida horizontalmente h unidades y verticalmente k unidades, de manera que el vertice se localice en (h,k).
- La gráfica de
. Si se utiliza el método de completar cuadrados, queda desarrollado de la siguiente manera:
Donde el primer termino es -h y el segundo termino es k.
Con eje de simetría en la recta  .
.
¿Que nos quiere decir? Que el vértice esta ubicado en: 
Ceros de la Función Cuadrática (Raíces)
Se dice que  es raíz de una función cuadrática
es raíz de una función cuadrática  , con
, con  si y solo si
si y solo si 
Aplicar la formula resolvente.
SI completamos con nuestros a, b, c que nos está dando el ejercicio en la resolvente nos dará 2 valores de x. Que llamamos arbitrariamente x1 y x2. Para x1 seleccionamos el símbolo + (más) y para el x2 el símbolo - (menos). Es indiferente en realidad, por cual de los dos arrancar.
Discriminante: 
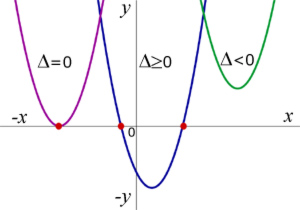
Caso A: Cuando el discriminante es MENOR a 0 , entonces la parabola NUNCA va a tocar al eje x.
Caso B: Cuando el discriminante es MAYOR a 0, entonces la parabola tocara DOS veces al eje x.
Caso C: Cuando el discriminante es IGUAL a 0, entonces la parabola tocara en UN punto al eje x.
--------------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------------
Forma canónica: 
Forma factorizada: Con a distinto de 0. Siendo x1 y x2 las raíces de la parábola.
Con a distinto de 0. Siendo x1 y x2 las raíces de la parábola.
Forma Polinomica:
Espero que les haya servido! / les haya interesado. Muchas gracias!
Si tenes ganas de recibir mas contenido de calidad, entonces hazte patreon! Tu ayuda me motiva. Si no podes permitírtelo, con hacer un click en alguna publicidad me ayudas muchísimo!
www.patreon.com/Apuntesing
Forma factorizada:
Forma Polinomica:
Espero que les haya servido! / les haya interesado. Muchas gracias!
Si tenes ganas de recibir mas contenido de calidad, entonces hazte patreon! Tu ayuda me motiva. Si no podes permitírtelo, con hacer un click en alguna publicidad me ayudas muchísimo!
www.patreon.com/Apuntesing
No hay comentarios:
Publicar un comentario