Función racional. Ecuación racional asociada.

Llamamos función racional a las funciones f: A→R tal que  donde P(x) y Q(x) son polinomios reales y .

Dominio:

El dominio de una función racional es el conjunto de todos los valores de la variable real que no anulan al denominador.

Dom f=A, donde 

Ejemplos:

  Donde x no puede ser 2.

 Donde x no puede ser -3 ni 0.

Representación Gráfica:

Asintotas verticales:

Si  es cero de Q(x) y no anula a P(x) , la recta de ecuación x=a es una asintota vertical.

Ejemplo:

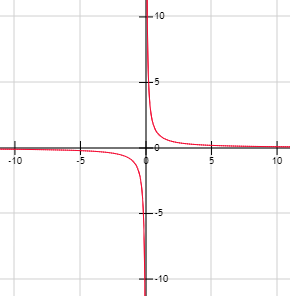
Tiene una asintota vertical en 0. Puesto que cuando x=0 La función tiende a infinito.

Asintotas horizontales:

Una función racional tiene asintota horizontal si el grado de P(x) es menor o igual que el grado de Q(x).

Ejemplo:

En este caso, y=0 es asintota horizontal de f(x).

Puesto que a medida que x va tomando valores cada vez mas grandes tanto para el lado positivo o negativo, la función se va aproximando al 0 en y.

Ceros de una función racional - Ecuaciones.

Las intersecciones del gráfico de una función racional f(x) con el eje x se producen para los valores de x que anulan la función, es decir, para aquellos que anulan al numerador y que pertenecen al dominio de f(x). Esos valores de x, si existen, son los ceros de f(x).

f: A→R/, entonces  es CERO de f(x) sii  es decir , .

Ejemplo:

,  para hallar los ceros, resolvemos la ecuación racional asociada:

 es decir, , y como -1 pertenece al dominio, entonces  es raíz de la función.

Funciones racionales y sus respectivas gráficas:

La gráfica de   tiene a la recta y=0 como Asintota horizontal y a la recta x=a como asintota vertical.