FLUJO DE AIRE Y OTROS GASES A TRAVÉS DE LAS BOQUILLAS
El diseño común de una boquilla implica una sección convergente a través de la cual pasa un fluido, de una región de presión mayor a otra de presión menor. La boquilla mostrada converge con suavidad y en forma gradual, y termina en su sección más pequeña, conocida como garganta.
Cuando el flujo de un gas circula con mucha lentitud, el calor de las cercanías se transfiere hacia o desde el gas, con el fin de mantener su temperatura constante. Dicho flujo recibe el nombre de isotérmico. Sin embargo, cuando el flujo circula con rapidez o cuando el sistema está muy bien aislado, puede transferirse muy poco calor hacia o desde el gas. En condiciones ideales, sin transferencia de calor, el flujo se denomina diabático. Los sistemas reales, en cierta manera, tienen un comportamiento entre isotérmico y adiabático. No obstante, para un flujo rápido a través de una boquilla se supondrá que es adiabático.
Flujo por una boquilla para procesos adiabáticos
El exponente k se denomina exponente adiabático, número adimensional, y su valor para el aire es 1.40
Puede demostrarse que la tasa de flujo alcanza un máximo en la relación de presión crítica.
Cuando se alcanza la relación de presión crítica, la velocidad del flujo en la garganta de la boquilla es igual a la velocidad del sonido en el gas.
Esta velocidad de flujo permanece constante, sin importar cuánto disminuya la presión delante de la corriente.
La velocidad supersónica, mayor que la del sonido, se obtiene sólo con una boquilla que primero converja y luego diverja.
El nombre número de Mach, se da a la relación de la velocidad real de flujo a la velocidad sónica.
La ecuación (18-11) debe emplearse para calcular el flujo en peso del gas que sale de un tanque a través de una boquilla convergente para valores de NM , 1.0, patm/p1 es mayor que la relación de presión crítica. Para NM = 1.0



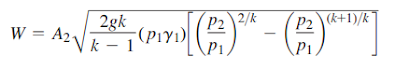


No hay comentarios:
Publicar un comentario